図形の求め方
基本的な図形の面積
面積公式一覧
三角形の面積=底辺×高さ÷2
正方形の面積=1辺×1辺。
長方形の面積=横×縦。
平行四辺形の面積=底辺×高さ。
台形の面積=(上底+下底)×高さ÷2
ひし形の面積=対角線×対角線÷2
円・おうぎ形
円の公式
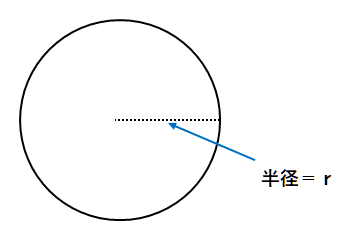
円周の長さ=2×円周率×半径。
ℓ=2πr
円の面積=半径×半径×円周率。
S=πr2
※S=面積,ℓ=円周の長さ。
おうぎ形の公式
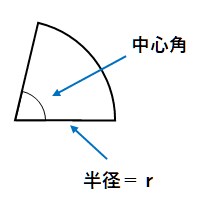
弧の長さ=円周×中心角360
ℓ=2πr×中心角360
おうぎ形の面積は
円の面積×中心角360
または,
12×半径×弧の長さ
S=πr2×中心角360
S=12ℓr
※S=面積,ℓ=弧の長さ。
正多面体
正多面体一覧。
正多面体は全部で5つ。
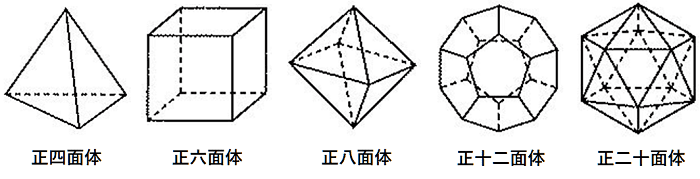
正四面体:すべての面が正三角形。
正六面体:すべての面が正方形。
正八面体:すべての面が正三角形。
正十二面体:すべての面が正五角形。
正二十面体:すべての面が正三角形。
投影図
投影図
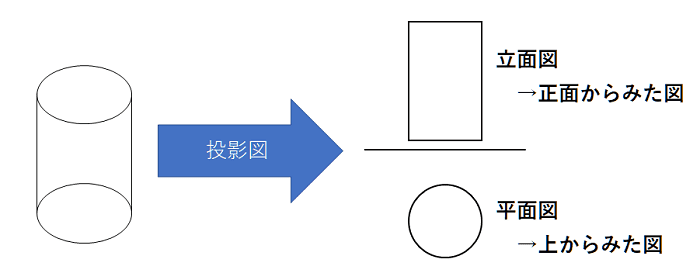
立面図:立体を正面からみた図。
平面図:立体を上からみた図。
立体の体積
柱体の体積
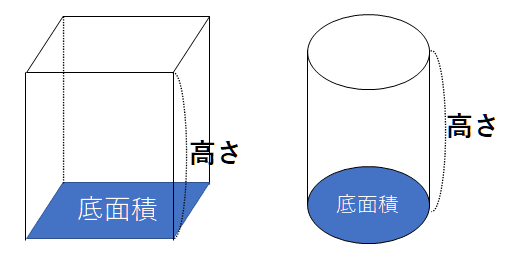
体積=底面積×高さ
錐体の体積
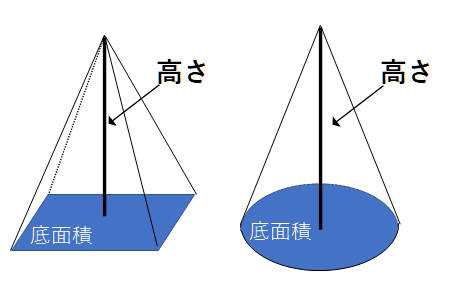
体積=底面積×高さ×13
立体の表面積
円柱の表面積
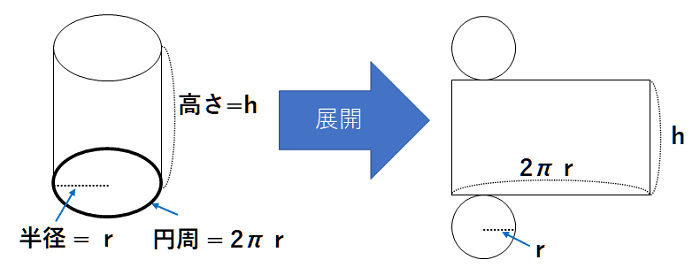
底面積=πr2
側面積=2πrh
表面積=底面積×2+側面積なので,
表面積=πr2×2+2πrh
円錐の表面積
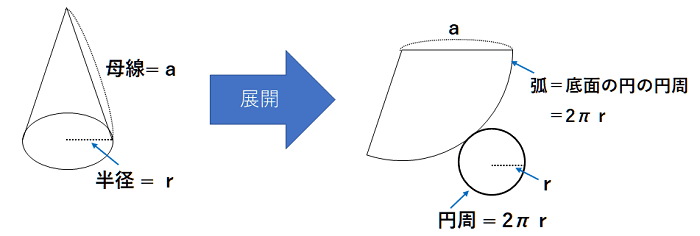
底面積=πr2
側面積(おうぎ形)=12×おうぎ形の半径×弧の長さ なので,
側面積==12a×2πr
表面積=πr2+12a×2πr
※側面積については約分が可能ですが、実際に解く際には計算の流れで自然に約分すると思いますので、約分しない形を残しておきます。
球
球の公式
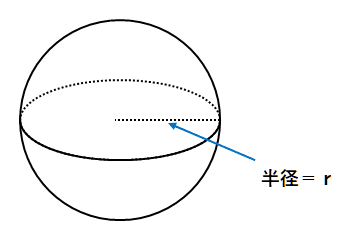
V=43πr3
S=4πr2
※V=体積,S=表面積。
合同条件
三角形の合同条件
①3組の辺がそれぞれ等しい。
②2組の辺とその間の角がそれぞれ等しい。
③1組の辺とその両端の角がそれぞれ等しい。
直角三角形の合同条件
①斜辺と1つの鋭角がそれぞれ等しい。
②斜辺と他の1辺がそれぞれ等しい。
図形の定義・性質
正三角形
定義:3辺が等しい三角形
よく使う性質
①正三角形の角度は全て等しい。
②正三角形の1つの角度は60°。
二等辺三角形
定義:2つの辺の長さが等しい三角形
よく使う性質
①二等辺三角形の底角は等しい。
②頂角の二等分線は底辺を垂直に二等分する。
平行四辺形
定義:2組の対辺がそれぞれ平行な四角形。
よく使う性質
①2組の対辺がそれぞれ等しい。
②2組の対角がそれぞれ等しい。
③対角線はそれぞれの中点で交わる。
平行四辺形になるための条件
①2組の対辺がそれぞれ平行。
②2組の対辺の長さがそれぞれ等しい。
③2組の対角の大きさがそれぞれ等しい。
④対角線がそれぞれの中点で交わる。
⑤1組の対辺が平行でその長さが等しい。
正方形
定義:4つの角がすべて等しく,4つの辺が全て等しい四角形。
よく使う性質
①正方形の1つの角度は90°。
長方形
定義:4つの角がすべて等しい四角形。
ひし形
定義:4つの辺がすべて等しい四角形。
よく使う性質
対角線は垂直に交わる。
相似条件
三角形の相似条件
①3組の辺の比がすべて等しい。
②2組の辺の比とその間の角がそれぞれ等しい。
③2組の角がそれぞれ等しい。
中点連結定理
中点連結定理
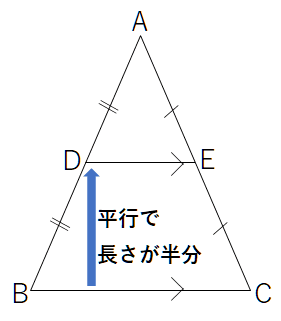
三角形ABCにおいて,点Dと点Eがそれぞれ辺ABと辺ACの中点の時,以下が成り立つ。
BC//DE。
DE=12BC
面積比・体積比
相似比な図形
相似比面積比体積比=a:b:cの時=a2:b2:c2=a3:b3:c3
高さが同じ三角形の面積比
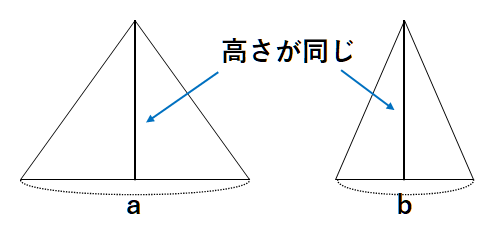
底辺の比面積比=a:b の時=a:b
三平方の定理
基本の公式(ピタゴラスの定理)
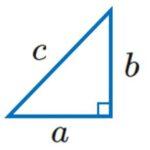
c2 = a2+b2
(斜辺の2乗) = (他の2辺の二乗の和)。
直角三角形の斜辺をc,他の辺の長さをそれぞれa,bとすると,この関係が成り立つ。
証明方法はここをクリック。
特別な三角形(角度と辺の比が決まっている直角三角形)
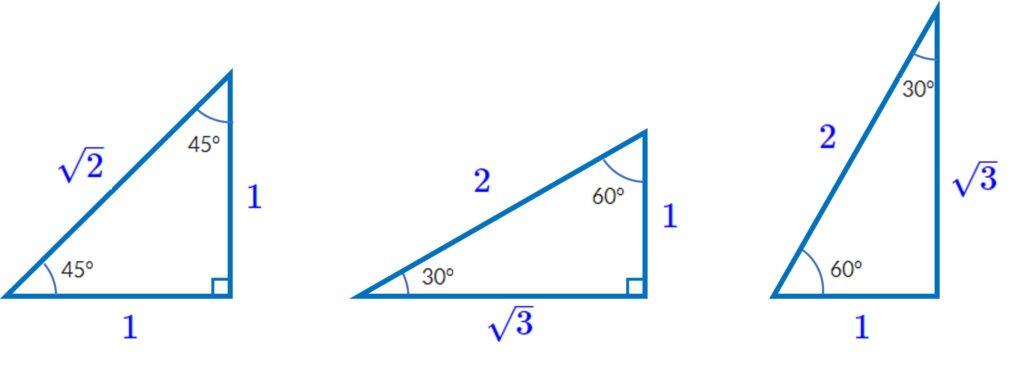
45°,45°,90度の直角三角形では,
1:1:2–√となる(2–√が斜辺)。
30°,60°,90°の直角三角形では,
1:2:3–√となる(2が斜辺)。
特別な三角形(ピタゴラス数)
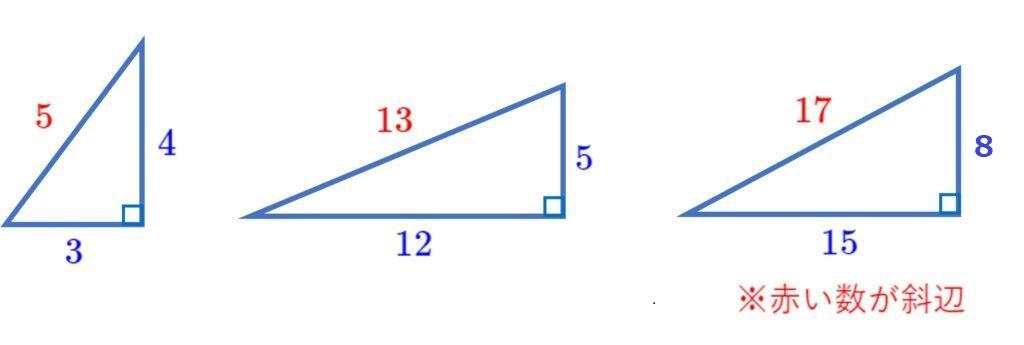
整数だけで,三平方が成り立つ(直角三角形の辺の長さが,すべて整数になる)組を「ピタゴラス数」という。無数に存在するが、この3つは出てくることが多い。(赤い数字は斜辺)
座標上の2点間の距離
(a.b)と(c,d)の距離は
(a−c)2+(b−d)2−−−−−−−−−−−−−−−√
円周角の定理
円周角の定理
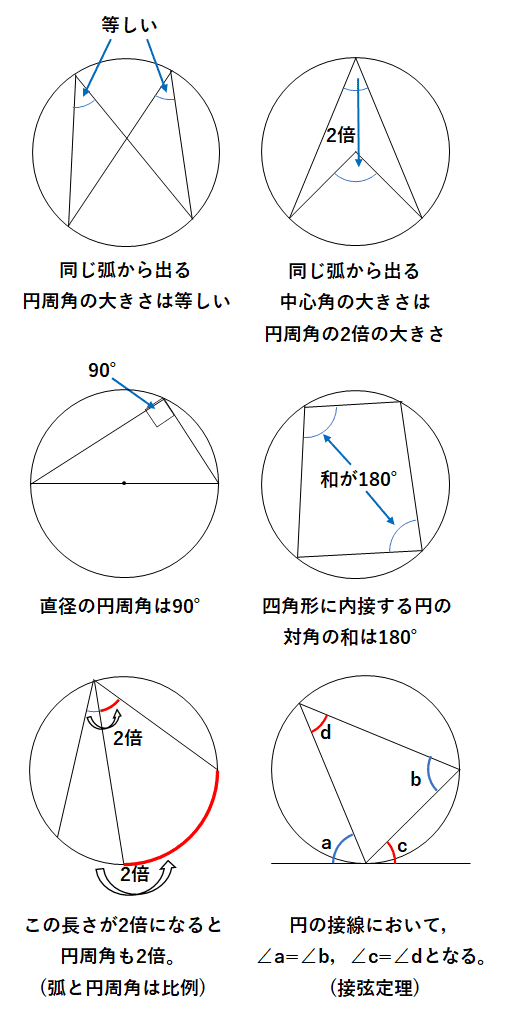
1件のコメント